PRUEBA DE HIPÓTESIS

PRUEBA DE HIPÓTESIS

Introducción

¿Cómo podemos comprobar una hipótesis? Para poder hacerlo primero debemos tener claro que una hipótesis es un enunciado que se realiza de manera previa al desarrollo de una determinada investigación, ésta puede ser verdadera o falsa.

Luego de esto debemos saber que en una prueba de hipótesis se examinan dos hipótesis opuestas sobre una población o  muestra: la hipótesis nula y la hipótesis alternativa; la hipótesis nula H_o es una suposición que se utiliza para negar o afirmar un suceso en relación a algún o algunos parámetros de una población o muestra, y la hipótesis alternativa H_i es lo que se podría pensar que es cierto, y sólo se puede formular cuando efectivamente hay otras posibilidades además de la hipótesis nula H_o.

Con base en los datos de la muestra, la prueba determina si se acepta o se rechaza la hipótesis nula H_o.

Un error común de percepción que siempre se presenta es que las pruebas estadísticas de hipótesis están diseñadas para seleccionar la más probable de dos hipótesis. Sin embargo, al diseñar una prueba de hipótesis, establecemos la hipótesis nula H_o como lo que queremos desaprobar. Puesto que establecemos el nivel de significancia para que sea pequeño antes del análisis (usualmente un valor de 0.05), cuando rechazamos la hipótesis nula H_o, tenemos prueba estadística de que la alternativa es verdadera.

En cambio, si no podemos rechazar la hipótesis nula H_o, no tenemos prueba estadística de que la hipótesis nula sea verdadera. Esto se debe a que no establecimos la probabilidad de aceptar equivocadamente la hipótesis nula H_o para que fuera pequeña.

      Prueba de hipótesis

Ahora nos toca determinar qué es una prueba de hipótesis:  

Es una regla que especifica si se puede aceptar o rechazar una afirmación acerca de una población dependiendo de la evidencia proporcionada por una muestra de datos.

En las pruebas de hipótesis se pueden dar dos tipos de errores en función de lo que nos aporta nuestra muestra y lo que objetivamente está ocurriendo en la realidad. Estos errores reciben el nombre de alfa y beta y se definen tal como se indica a continuación:

El error alfa α o tipo I, es el que se comete al rechazar la hipótesis nula H_o siendo cierta. Es decir, aceptamos que existen diferencias entre tratamientos cuando en realidad no las hay.

El error beta β o tipo II, es el error que se comete al aceptar la hipótesis nula H_o siendo falsa. Es decir, existe una diferencia real entre tratamientos pero no se ha podido rechazar la hipótesis nula H_o.

Como lo que ocurre en la realidad es desconocido, lo único que podemos acotar es la probabilidad de equivocarnos.

	Verdad acerca de la población
Decisión basada en la muestra	Ho es verdadera	Ho es falsa
No rechazar Ho	Decisión correcta (probabilidad = 1 – α)	Error tipo II – no rechazar Ho cuando es falsa (probabilidad = β)
Rechazar Ho	Error tipo I – rechazar Ho cuando es verdadera (probabilidad = α)	Decisión correcta (probabilidad = 1 – β)

           Pruebas continuas o paramétricas

Su cálculo implica una estimación de los parámetros de la población con base en muestras estadísticas, mientras más grande sea la muestra más exacta será la estimación.

Este tipo de pruebas tiene las siguientes ventajas:

    Ø  Posee más poder de eficiencia.

    Ø  Es más sensible a los rasgos de los datos recolectados. 

    Ø  Existen menos posibilidades de errores.

         Ø  Dan probabilidades estadísticas bastante exactas.

Prueba "Z"

Una prueba Z es una prueba de hipótesis basada en el estadístico Z, que sigue la distribución normal estándar bajo la hipótesis nula.

La prueba Z más simple es la prueba Z de 1 muestra, la cual evalúa la media de una población normalmente distribuida con varianza conocida. Por ejemplo, el gerente de una fábrica de caramelos desea saber si el peso medio de un lote de cajas de caramelos es igual al valor objetivo de 10 onzas. Partiendo de datos históricos, el gerente sabe que la máquina de llenado tiene una desviación estándar de 0.5 onzas, así que utiliza este valor como la desviación estándar de la población en una prueba Z de 1 muestra.

También puede utilizar las pruebas Z para determinar si las variables predictoras en los análisis probit y en la regresión logística tienen un efecto significativo en la respuesta. La hipótesis nula indica que el predictor no es significativo.

También tiene la opción de utilizar una prueba Z para realizar una aproximación a la normal para las pruebas de tasa de Poisson y las pruebas de proporciones. Estas aproximaciones a la normal son válidas cuando el tamaño de la muestra y el número de eventos son adecuadamente grandes.

Para que la prueba Z sea ​​aplicable, se deben cumplir ciertas condiciones.

• Los parámetros molestos deben ser conocidos o estimados con alta precisión (un ejemplo de un parámetro molesto sería la desviación estándar en una prueba de ubicación de una muestra). Las pruebas Z se centran en un solo parámetro y tratan a todos los demás parámetros desconocidos como si estuvieran fijos en sus valores reales. En la práctica, debido al teorema de Slutsky , se puede justificar el "complemento" de estimaciones coherentes de los parámetros de molestia. Sin embargo, si el tamaño de la muestra no es lo suficientemente grande como para que estas estimaciones sean razonablemente precisas, la prueba Z puede no tener un buen desempeño.
• El estadístico de prueba debe seguir una distribución normal . En general, se apela al teorema del límite central para justificar que se supone que una estadística de prueba varía normalmente. Hay una gran cantidad de investigaciones estadísticas sobre la cuestión de cuándo un estadístico de prueba varía aproximadamente normalmente. Si la variación del estadístico de prueba es fuertemente no normal, no se debe usar una prueba Z.

Una prueba Z es cualquier prueba estadística para la cual la distribución del estadístico de prueba bajo la hipótesis nula puede aproximarse a una distribución normal . Debido al teorema del límite central , muchas estadísticas de prueba se distribuyen aproximadamente normalmente para muestras grandes. Para cada nivel de significación, el Z -test tiene un único valor crítico (por ejemplo, 1,96 para el 5% dos colas) que hace que sea más conveniente que el de Student t -testque tiene valores críticos separados para cada tamaño de muestra. Por lo tanto, muchas pruebas estadísticas pueden realizarse convenientemente como pruebas Z aproximadas si el tamaño de la muestra es grande o se conoce la varianza de la población. Si la varianza de la población es desconocida (y, por lo tanto, debe estimarse a partir de la propia muestra) y el tamaño de la muestra no es grande (n <30), la prueba t de Student puede ser más apropiada.

 Una empresa está interesada en lanzar un nuevo producto al negocio de cremas para la piel Tras realizar una campaña publicitaria, se toma la muestra de 1 000 habitantes, de los cuales, 25 no conocían el producto. A un nivel de significación del 1% ¿apoya el estudio las siguientes hipótesis?

• a. Más del 3% de la población  no conoce el nuevo producto.
• b. Menos del 2% de la población no conoce el nuevo producto
• Datos:
  n = 1000
  x = 25
  
  
• 
  
  
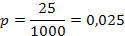
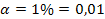
• Donde:
  x = ocurrencias
  n = observaciones
  = proporción de la muestra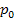
  = proporción propuesta
  Solución:
  a)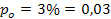
  
  
  
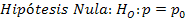
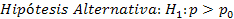  a = 0,01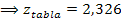 

Propuesto:

CCuando las ventas medias, por establecimiento autorizado, de una marca de relojes caen por debajo las
1 150,000 unidades mensuales, se considera razón suficiente para lanzar una campaña publicitaria que active las ventas de esta marca. Para conocer la evolución de las ventas, el departamento de marketing realiza una encuesta a 50 establecimientos autorizados, seleccionados aleatoriamente, que facilitan la cifra de ventas del último mes en relojes de esta marca. A partir de estas cifras se obtienen los siguientes resultados: media = 165.411,8 unidades., desviación estándar = 22.827,5 unidades. Suponiendo que las ventas mensuales por establecimiento se distribuyen normalmente; con un nivel de significación del 4% y en vista a la situación reflejada en los datos. ¿Se considerará oportuno lanzar una nueva campaña publicitaria?

PRUEBA T DE STUDENT

      Definición

    Una variable con distribución t de Student se define como el cociente entre una variable normal estandarizada y la raíz cuadrada positiva de una variable 2 dividida por sus grados de libertad. Se aplica cuando la población estudiada sigue una distribución normal pero el tamaño muestral es demasiado pequeño como para que el estadístico en el que está basada la inferencia esté normalmente distribuido, utilizándose una estimación de la desviación típica en lugar del valor real. Es utilizado en análisis discriminante.

   La prueba t de student es cualquier prueba de hipótesis estadística en la que la se comprueba si la variable sigue una distribución t de Student bajo la hipótesis nula.

    La prueba t se aplica con mayor frecuencia cuando la estadística de prueba seguiría una distribución normal si se conociera el valor de un término de escala en la estadística de prueba. Cuando se desconoce el término de escala y es reemplazado por un estimado basado en los datos, las estadísticas de prueba (bajo ciertas condiciones) siguen una distribución t de Student. La prueba t se suele usar, por ejemplo, para determinar si dos conjuntos de datos son significativamente diferentes entre sí.

                        Empleo de la prueba t de student 

• El test de locación de muestra única por el cual se comprueba si la media de una población distribuida normalmente tiene un valor especificado en una hipótesis nula.
• El test de locación para dos muestras, por el cual se comprueba si las medias de dos poblaciones distribuidas en forma normal son iguales. Todos estos test son usualmente llamados test t de Student, a pesar de que estrictamente hablando, tal nombre sólo debería ser utilizado si las varianzas de las dos poblaciones estudiadas pueden ser asumidas como iguales; la forma de los ensayos que se utilizan cuando esta asunción se deja de lado suelen ser llamados a veces como prueba t de welch Estas pruebas suelen ser comúnmente nombradas como pruebas t desapareadas o de muestras independientes, debido a que tienen su aplicación mas típica cuando las unidades estadísticas que definen a ambas muestras que están siendo comparadas no se superponen.
• El test de hipótesis nula por el cual se demuestra que la diferencia entre dos respuestas medidas en las mismas unidades estadísticas es cero. Por ejemplo, supóngase que se mide el tamaño del tumor de un paciente con cáncer. Si el tratamiento resulta efectivo, lo esperable seria que el tumor de muchos pacientes disminuyera de tamaño luego de seguir el tratamiento. Esto con frecuencia es referido como prueba t de mediciones apareadas o repetidas.
• El test para comprobar si la pendiente de una regresión lineal difiere estadísticamente de cero.

¿Cómo se deduce una distribución de “t”?

    ·                     Extraigo K muestras de tamaño n < 30.

    ·                     Calculo para cada muestra el valor de “t”.

    ·                     Grafique la distribución para cada tamaño muestral

               CARACTERISTICAS DE PRUEBA T DE STUDENT

       Condiciones:

·         Se utiliza en muestras de 30 o menos elementos. n<30

·         La desviación estándar de la población no se conoce.

·         El valor de α no se divide como en la normal (Z).

·         Se calcula los grados de libertad.

       Diferencias:

·         La distribución t student es menor en la media y más alta en los extremos que una distribución normal.

·         Tiene proporcionalmente mayor parte de su área en los extremos que la distribución normal.

        Nivel de significación:

      Grados de libertad:

     Existe una distribución t para cada tamaño de la muestra, por lo que “Existe una distribución para cada uno de los grados de libertad”.

     Los grados de libertad son el número de valores elegidos libremente.

    Dentro de una muestra para distribución t student los grados de libertad se calculan de la siguiente manera:

     GL=n – 1 

           EJEMPLO

    Con un nivel de significancia de 5% se selecciona de manera aleatoria tres paquetes de croquetas (bultos) alimento para perros,  de cada uno de los cinco pedidos. Al pesar los 15 paquetes se obtiene la media de = 49.4 y una desviación estándar de  S² = 1.2

      Establecer el estadístico de prueba calculado de acuerdo a la expresión

      Sustituyendo datos queda:

      Por tanto concluimos que 

    1.-  se encuentra en la región de rechazo  que por lo cual  se considera que existe menor cantidad de croquetas en los paquetes.

     2.- No cumple con lo que  pide.

     CASOS

1.    DIFERENCIA DE MEDIAS 

    Un fabricante de focos afirma que sus producto durará un promedio de 500 horas de trabajo. Para conservar este promedio esta persona verifica 25 focos cada mes. Si el valor y calculado cae entre –t 0.05 y t 0.05, él se encuentra satisfecho con esta afirmación. ¿Qué conclusión deberá él sacar de una muestra de 25 focos cuya duración fue?:

 

    Se puede concluir que la media poblacional no es 500, porque la muestra poblacional está por encima de esta, y por lo tanto debería estar por encima de 500.

2.    DIFERENCIA DE MEDIDAS PARA 2 POBLACIONES

3.    DIFERENCIA DE PROPORCIONES

4.    DIFERENCIA DE POBLACIÓN

      EJERCICIOS PARA LA PRUEBA  t  DE STUDENT

    1.- Se desea determinar si los promedios de puntos de calificación (PPC) son diferentes para niños y niñas. Se considera que el PPC se distribuye normalmente con varianza idéntica para ambos sexos. Dos muestras independientes de 5 estudiantes cada una proporcionan lo siguiente:

        PPC para niños: 2.9   3.1   2.7   3.3   3.0

        PPC para niñas: 3.6   2.8   3.6   3.2   2.8

a)    Utilizando α = 0.05, pruébese la hipótesis de que el PPC medio para niños es el mismo que el PPC medio para niñas, contra la hipótesis alternativa de que las dos medias son diferentes.

b)    Obténganse los límites de confianza del 95% para la verdadera diferencia entre las dos medias poblacionales.

     2.- Se desea determinar si una clase de 16 estudiantes pueden desempeñarse igualmente bien en español que en matemáticas. Las calificaciones de prueba listadas a continuación no son independientes:

               Estudiante            Español            Matemáticas

           _________________________________________

                A                         84                        84

                B                         55                        57

                C                         85                        90

                D                         98                        97

                E                          80                       74

                F                          55                       53

               G                          80                       75

               H                          64                        63

               I                            91                       90

               J                            85                       82

               K                           90                       88

               L                           94                        98

               M                          75                        77

               N                          86                         90

               O                          91                         85

               P                           92                         86

a)    Considerando que las calificaciones de prueba se distribuyen normalmente, pruébese la hipótesis de que la puntuación media de la población en español es la misma que en matemáticas contra la hipótesis alternativa de que son diferentes para α = 0.05.

b)    Establézcase el intervalo de confianza del 95 % para la verdadera diferencia.

   3.- Un productor de azúcar empaca ésta en bolsas de papel, cada una de las cuales, supuestamente contiene 5 Lb ( 80 oz ) de azúcar. De modo periódico se toma una muestra aleatoria de 100 bolsas para determinar si contienen la cantidad correcta. Si la media maestral  X difiere significativamente de 80 oz se considera que el proceso de empaque está funcionando en forma inadecuada. Supóngase que una muestra de 100 bolsas proporciona una media de 79 oz y una desviación estándar de 5 oz ¿Está funcionando adecuadamente el proceso en α= 0.05?

                                      DISTRIBUCION HIPERGEOMETRICA

     La distribución hipergeométrica es especialmente útil en todos aquellos casos en los que se extraigan muestras o se realicen experiencias repetidas sin devolución del elemento extraído o sin retornar a la situación experimental inicial.
Es una distribución fundamental en el estudio de muestras pequeñas de poblaciones pequeñas y en el cálculo de probabilidades de juegos de azar. Tiene grandes aplicaciones en el control de calidad para  procesos experimentales en los que no es posible retornar a la situación de partida.
Las consideraciones a tener en cuenta en una distribución hipergeométrica:

o    El proceso consta de "n" pruebas, separadas o separables de entre un conjunto de "N" pruebas posibles.

o  Cada una de las pruebas puede dar únicamente dos resultados mutuamente excluyentes.

o     El número de individuos que presentan la característica A (éxito) es "k".

o     En la primera prueba las probabilidades son: P(A)= p y P(A)= q; con p+q=1.

En estas condiciones, se define la variable aleatoria X = “nº de éxitos obtenidos”. La función de probabilidad de esta variable sería:

      EJEMPLO 1:
Supongamos la extracción aleatoria de 8 elementos de un conjunto formado por 40 elementos totales (cartas baraja española) de los cuales 10 son del tipo A (salir oro) y 30 son del tipo complementario (no salir oro).
Si realizamos las extracciones sin devolver los elementos extraídos y llamamos X al número de elementos del tipo A (oros obtenidos) que extraemos en las 8 cartas; X seguirá una distribución hipergeométrica de parámetros 40 , 8 , 10/40.H(40,8,0,25).
Para calcular la probabilidad de obtener 4 oros:

      EJEMPLO 2:

     En una jaula hay 30 pericos alemanes y 20 pericos ingleses si extraemos 10     pericos al azar, calcular la probabilidad de que 3 de ellos hablen ingles.

              Pruebas discretas o no paramétricas 

    Se denominan pruebas no paramétricas aquellas que no presuponen una distribución de probabilidad para los datos, por ello se conocen como de distribución libre. 

    En la mayor parte de ellas los resultados estadísticos se derivan únicamente a partir de procedimientos de ordenación y recuento, por lo que su base lógica es de fácil comprensión.

Las ventajas de estas pruebas son:

   Ø  Los métodos no paramétricos pueden ser aplicados a una amplia variedad de situaciones porque ellos no tienen los requisitos rígidos.

    Ø  Pueden frecuentemente ser aplicados a datos no numéricos, tal como el género de los que contestan una encuesta.

    Ø  Usualmente involucran simples cómputos que los métodos paramétricos y son por lo tanto, más fáciles para entender y aplicar.

Distribución de Poisson

    En teoría de probabilidad y estadística, la distribución de Poisson es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la probabilidad de que ocurra un determinado número de eventos durante cierto período de tiempo. Concretamente, se especializa en la probabilidad de ocurrencia de sucesos con probabilidades muy pequeñas, o sucesos "raros".

    En la inspección de hojalata producida por un proceso electrolítico continuo, se identifican 0.2 imperfecciones en promedio por minuto. Determine las probabilidades de identificar a) una imperfección en 3 minutos, b) al menos dos imperfecciones en 5 minutos, c) cuando más una imperfección en 15 minutos.

Solución:

a)      x = variable que nos define el número de imperfecciones en la hojalata por cada 3 minutos = 0, 1, 2, 3, ...., etc., etc.

 = 0.2 x 3 =0.6 imperfecciones en promedio por cada 3 minutos en la hojalata

b)      x = variable que nos define el número de imperfecciones en la hojalata por cada 5 minutos = 0, 1, 2, 3, ...., etc., etc.

 = 0.2 x 5 =1 imperfección en promedio por cada 5 minutos en la hojalata

                 =1-(0.367918+0.367918) = 0.26416

c)      x = variable que nos define el número de imperfecciones en la hojalata por cada 15 minutos = 0, 1, 2, 3, ....., etc., etc.

 = 0.2 x 15 = 3 imperfecciones en promedio por cada 15 minutos en la hojalata

 = 0.0498026 + 0.149408 = 0.1992106

            Distribución binomial    

    En estadística, la distribución binomial es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos. Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, solo dos resultados son posibles. A uno de estos se denomina «éxito» y tiene una probabilidad de ocurrencia p y al otro, «fracaso», con una probabilidad²​ q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.

                          

      La última novela de un autor ha tenido un gran éxito, hasta el punto de que el 80% de los lectores ya la han leído. Un grupo de 4 amigos son aficionados a la lectura:

       1 ¿Cuál es la probabilidad de que en el grupo hayan leído la novela 2 personas?

       B (4, 0.2) p = 0.8 q = 0.2

       2 ¿Y cómo máximo 2?

  

           Chi-cuadrado (X²)

   Una prueba de chi-cuadrada es una prueba de hipótesis que compara la distribución observada de los datos con una distribución esperada de los datos.

     El estadístico de chi-cuadrada es una medida de la divergencia entre la distribución de los datos y una distribución esperada o hipotética seleccionada. Por ejemplo, se utiliza para:

·         Probar la independencia o determinar la asociación entre variables categóricas. Por ejemplo, si usted tiene una tabla de dos factores de resultados electorales basada en el sexo de los votantes, los estadísticos de chi-cuadrada pueden ayudar a determinar si un voto es independiente del sexo del votante o si existe alguna asociación entre voto y sexo. Si el valor p asociado con el estadístico de chi-cuadrada es menor que el nivel de significancia (α) seleccionado, la prueba rechaza la hipótesis nula de que las dos variables son independientes.

·         Determinar si un modelo estadístico se ajusta adecuadamente a los datos. Si el valor p asociado al estadístico de chi-cuadrada es menor que el nivel de significancia (α) seleccionado, la prueba rechaza la hipótesis nula de que el modelo se ajusta a los datos.

    Al contrario que la normal, la función de densidad de la chi-cuadrado solo tiene valores positivos, por lo que es asimétrica con una larga cola hacia la derecha. Claro que la curva se va haciendo cada vez más simétrica al aumentar los grados de libertad, pareciéndose cada vez más a una distribución normal.

       Historia de la prueba chi-cuadrado

      Karl Pearson

     Nació el 27 de marzo de 1857 en Londres y falleció el 27 de abril de 1937 en la misma ciudad, fue un prominente científico, matemático y pensador británico, que estableció la disciplina de la estadística matemática. Desarrolló una intensa investigación sobre la aplicación de los métodos estadísticos en la biología y fue el fundador de la bioestadística.

    En 1900 publicó su prueba de Chi-cuadrado, una medida de la bonanza de una cierta distribución al ajustarse a un grupo determinado de datos. La prueba permite determinar, entre otras cosas, si dos caracteres hereditarios eran transmitidos de forma dependiente o independiente. Los análisis de Pearson se han revelado como imprescindibles para una correcta interpretación de los datos estadísticos.

     La prueba χ² de Pearson se considera una prueba no paramétrica que mide la discrepancia entre una distribución observada y otra teórica (bondad de ajuste), indicando en qué medida las diferencias existentes entre ambas, de haberlas, se deben al azar en el contraste de hipótesis. También se utiliza para probar la independencia de dos variables entre sí, mediante la presentación de los datos en tablas de contingencia.

La fórmula que da el estadístico es la siguiente: 

{\displaystyle \chi ^{2}=\sum _{i}{\frac {(\mathrm {observada} _{i}-\mathrm {teorica} _{i})^{2}}{\mathrm {teorica} _{i}}}}      Cuanto mayor sea el valor de {\displaystyle \chi ^{2}}XXxX, menos verosímil es que la hipótesis nula (que asume la igualdad entre ambas distribuciones) sea correcta. De la misma forma, cuanto más se aproxima a cero el valor de chi-cuadrado, más ajustadas están ambas distribuciones.

      Los grados de libertad V vienen dados por:  V = (r – 1) (k – 1)

 

            Ejercicios #1.

    La siguiente tabla refleja la cantidad de estudiantes, según la calificación obtenida de dos universidades:

	Insuficiente	Básico	Satisfactorio	Total
UEES	5	11	7	23
UG	20	32	3	55
Total	25	43	10	78

      ¿Influye el tipo de universidad en la calificación obtenida?

      Margen de error: 0,05

                7) Toma de decisión.

     Se rechaza la hipótesis nula (H_o), es decir el tipo de universidad si influye en las calificaciones, o lo que es equivalente la diferencia observada no es producto del azar.

         Ejercicio #2.

   Se desea estudiar hasta qué punto existe relación entre el tiempo de residencia de inmigrantes en nuestro país y su percepción de integración. Se dispone de una muestra pequeña de 230 inmigrantes a los que se les evaluó en ambas variables obteniéndose la siguiente tabla de frecuencias observadas.

Tiempo de residencia	Grado de integración		Total
	Bajo	Alto
Más tiempo	40	90	130
Menos tiempo	90	10	100
Total	130	100	230

      Nivel de confianza: 95%

                                                 F de Fisher 

     Características

·         Existe una distribución F diferente para cada combinación de tamaño de muestra y número de muestras. Por tanto, existe una distribución F que se aplica cuando se toman cinco muestras de seis observaciones cada una, al igual que una distribución F diferente para cinco muestras de siete observaciones cada una.

     A propósito de esto, el número distribuciones de muestreo diferentes es tan grande que sería poco práctico hacer una extensa tabulación de distribuciones. Por tanto, como se hizo en el caso de la distribución t, solamente se tabulan los valores que más comúnmente se utilizan.

      En el caso de la distribución F, los valores críticos para los niveles 0,05 y 0,01 generalmente se proporcionan para determinadas combinaciones de tamaños de muestra y número de muestras.

·         La distribución es continua respecto al intervalo de 0 a + ∞

       La razón más pequeña es 0. La razón no puede ser negativa, ya que ambos términos de la razón F están elevados al cuadrado.

     Por otra parte, grandes diferencias entre los valores medios de la muestra, acompañadas de pequeñas variancias muestrales pueden dar como resultado valores extremadamente grandes de la razón F.

·         La forma de cada distribución de muestreo teórico F depende del número de grados de libertad que estén asociados a ella. Tanto el numerador como el denominador tienen grados de libertad relacionados.

     Historia de la razón F

      Esta razón F fue creada por Ronald Fisher (1890-1962), matemático británico, cuyas teorías estadísticas hicieron mucho más precisos los experimentos científicos. Sus proyectos estadísticos, primero utilizados en biología, rápidamente cobraron importancia y fueron aplicados a la experimentación agrícola, médica e industrial. Fisher también contribuyó a clarificar las funciones que desempeñan la mutación y la selección natural en la genética, particularmente en la población humana.

      El valor estadístico de prueba resultante se debe comparar con un valor tabular de F, que indicará el valor máximo del valor estadístico de prueba que ocurría si H0 fuera verdadera, a un nivel de significación seleccionado. Antes de proceder a efectuar este cálculo, se debe considerar las características de la distribución F.

      Determinación de los grados de libertad

       Los grados de libertad para el numerador y el denominador de la razón F se basan en los cálculos necesarios para derivar cada estimación de la variancia de la población. La estimación intermediante de variancia (numerador) comprende la división de la suma de las diferencias elevadas al cuadrado entre el número de medias (muestras) menos uno, o bien, k - 1. Así, k - 1 es el número de grados de libertad para el numerador.

    En forma semejante, el calcular cada variancia muestral, la suma de las diferencias elevadas al cuadrado entre el valor medio de la muestra y cada valor de la misma se divide entre el número de observaciones de la muestra menos uno, o bien, n - 1. Por tanto, el promedio de las variancias muestrales se determina dividiendo la suma de las variancias de la muestra entre el número de muestras, o k. Los grados de libertad para el denominador son entonces, k(n - l).      

        Ejercicio #1

     Los pesos en kg por 1,7 m de estatura se ilustran en la siguiente tabla. La finalidad es determinar si existen diferencias reales entre las cuatro muestras.

      Nivel de significancia de 0,05

Observación	Muestra
	1	2	3	4
1	70	74	68	75
2	75	77	70	70
3	74	70	65	73
4	72	80	60	72
5	68	72	72	71
6	59	76	73	72

   

   

   

   Integrantes:  

Avilés Paola

Zambrano Daniela

Romero Mario

çOlaya David

Crasfford Ginger

n